Novembre/Dicembre 2015
n
Automazione e Strumentazione
CONTROLLO
tecnica
84
in tempo reale delle operazioni di movimentazione eseguite dal
forno che prevedono, ad esempio, lo sfornamento di una billetta,
il passo in avanti del forno (per consentire l’ingresso di una nuova
billetta), il posizionamento di una nuova billetta sulla via rulli in
ingresso al forno, il successivo posizionamento della stessa sulla
prima posizione all’interno del forno, ecc.
Il corretto tracciamento delle billette è garantito processando
alcuni segnali disponibili a PLC, quali: pirometro ottico in
ingresso al forno, fotocellule installate nel percorso delle billette,
trigger che identifica l’esecuzione del passo del forno, pirometro
ottico in uscita al forno, ecc. In questo modo, l’algoritmo di tra-
cking sarà in grado di identificare tutte le operazioni eseguite in
campo compresi, ad esempio, gli eventuali spazi vuoti che ven-
gono predisposti dagli operatori tra una billetta e l’altra per esi-
genze produttive (per separare due differenti prodotti realizzati);
l’algoritmo è inoltre in grado di gestire situazioni anomale che si
possono verificare durante il normale funzionamento, come l’in-
caglio di una billetta durante il suo tragitto. La
►
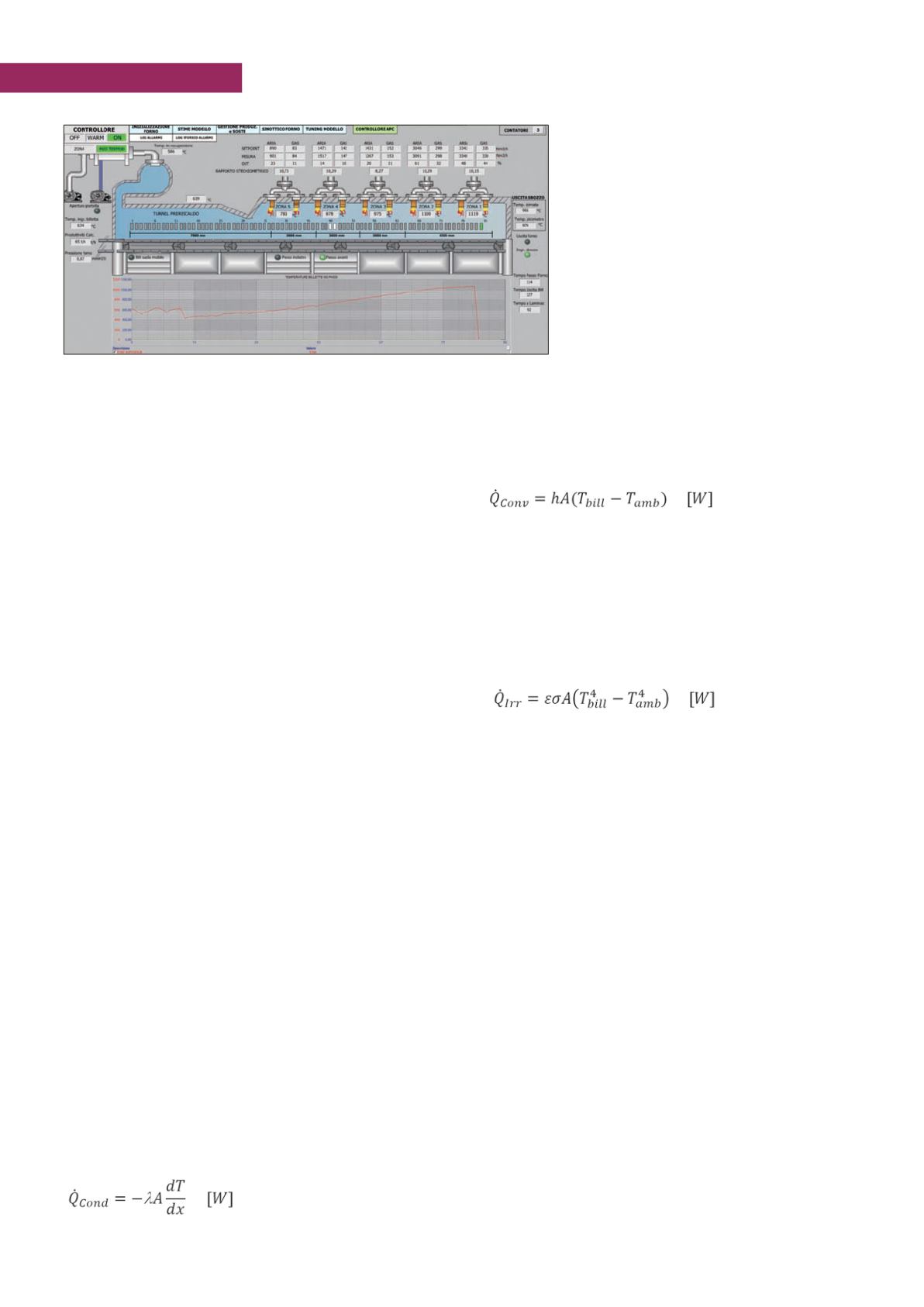
figura 2
mostra
una pagina dell’interfaccia operatore dell’APC, in cui sono visua-
lizzate alcune informazioni dell’algoritmo di tracking; oltre alle
misure provenienti dagli strumenti descritti nella seconda sezione
(Descrizione del processo), è possibile visualizzare le billette pre-
senti nel forno: in grigio sono rappresentati i posti del forno occu-
pati da billette, in bianco i posti vuoti ed in verde le billette che
hanno raggiunto la temperatura di sfornamento desiderata.
Modello agli elementi finiti (fem)
Il modello termodinamico agli elementi finiti (FEM) implementato
all’interno dell’APC è utilizzato per stimare il profilo di riscaldo
di ciascuna billetta all’interno del forno. Il modello deriva da una
discretizzazione agli elementi finiti della billetta, applicando le
equazioni di diffusione termica tra i diversi strati con condizioni
al contorno convettive (al di fuori del forno) e di irraggiamento
(all’interno del forno); questo approccio è impiegato solitamente
in problemi di trasmissione del calore ([5]).
L’equazione di diffusione, applicata ad ogni strato di ciascuna bil-
letta, segue il noto postulato di Fourier:
modello di conduzione
dove
A
[m
2
] è l’area della sezione della billetta
normale alla direzione di trasmissione del calore,
λ
[W/(m∙K)] è la conducibilità termica della billetta,
dT
[K] è la differenza di temperatura dello strato,
dx
[m], considerato. Il modello di conduzione
può essere applicato scegliendo arbitrariamente il
numero di strati con cui rappresentare ciascuna bil-
letta; un vincolo che l’algoritmo controlla riguarda
la scelta del numero degli strati in modo da garan-
tire la convergenza della soluzione del modello di
conduzione in relazione ai parametri fisici delle
stessa.
Le condizioni al contorno seguiranno i ben noti
modelli termodinamici di convezione (al di fuori del forno) e
irraggiamento (all’interno del forno):
Modello di convezione
dove
A
[m
2
] è l’area della superficie esposta,
h
[W/(m
2
∙K)] è il
coefficiente di scambio convettivo,
T
bill
[°C] è la temperatura
della billetta e
T
amb
[°C] è la temperatura del fluido che circonda
la billetta.
Modello di irraggiamento
dove
A
[m
2
] è l’area della superficie esposta,
ε
(valore compreso
tra 0 e 1) è il fattore di emissività,
σ
[W/(m
2
∙K
4
)] è la costante di
Stefan-Boltzmann,
T
bill
[K] è la temperatura della billetta e
T
amb
[K] è la temperatura dell’ambiente nel quale la billetta è inserita
(zone del forno).
I coefficienti di scambio termico impiegati nei modelli precedenti
non sono fissati ad un valore costante, ma sono stimati in linea
(all’interno di un range fisicamente accettabile) al fine di assorbire
eventuali incertezze non modellate. La stima è realizzata mediante
un identificatore non lineare che tiene in considerazione la “sto-
ria passata” (tutti i passaggi avvenuti all’interno e all’esterno
del forno) della billetta in uscita. In base alle misure effettuate a
valle del forno (assorbimenti elettrici delle gabbie di laminazione
e temperatura misurata dal pirometro ottico), è eseguita la stima
dei coefficienti di scambio termico della billetta appena uscita
dal forno tali che la stima di temperatura sia allineata alla misura
reale; i nuovi coefficienti sono poi applicati opportunamente a
tutte le altre billette contenute nel forno ricalcolando la loro stima
attuale. Le correzioni del modello si riflettono quindi in variazioni
nei coefficienti di scambio termico dei modelli termodinamici pre-
cedentemente illustrati: questo aspetto costituisce un aspetto molto
innovativo, in quanto è incrementata l’affidabilità della stima del
modello termodinamico e, di conseguenza, dell’algoritmo di con-
trollo. Inoltre algoritmi di
max innovation
e
innovation threshold
garantiscono perturbazioni smooth ai coefficienti ristimati; infine
Figura 2 - Display dell’interfaccia APC che mostra un dettaglio del forno