CONTROLLO
tecnica
Maggio 2014
■
Automazione e Strumentazione
82
L’azione in anello aperto risulta molto utile per migliorare le prestazioni di
reazione ai disturbi misurabili. In questo contributo si forniscono gli elementi
teorici per approfondire la sintesi del compensatore e migliorare le sue
prestazioni, indicando anche una metodologia per la sua auto-sintonia.
Massimiliano Veronesi
Antonio Visioli
L’importanza di portarsi avanti
I nostri nonni ci raccomandavano spesso “chi ha
tempo non aspetti tempo”, invitandoci a portarci
avanti nel fare i compiti in modo da non dover
poi affrontare eventuali sovraccarichi di lavoro
che ci avrebbero sottratto ai divertimenti tipici
nella vita dei bambini. Suggerimento simile vale
anche per i controllori, ove una azione in anello
aperto (feedforward) può consentire di miglio-
rare sensibilmente le prestazioni del regolatore,
che di per sé agisce in retroazione (feedback); è
infatti intuitivo comprendere che, sapendo che
un intervenuto cambiamento (disturbo) influirà
sulla grandezza da controllare, iniziare a reagire
prontamente sarà meglio che attendere che i suoi
effetti si manifestino sulla variabile misurata. Il
tipico caso è quello del controllo della tempera-
tura all’uscita di uno scambiatore di calore: la
variazione della portata in entrata rappresenta un
disturbo che può essere efficacemente compen-
sato attraverso l’azione in anello aperto.
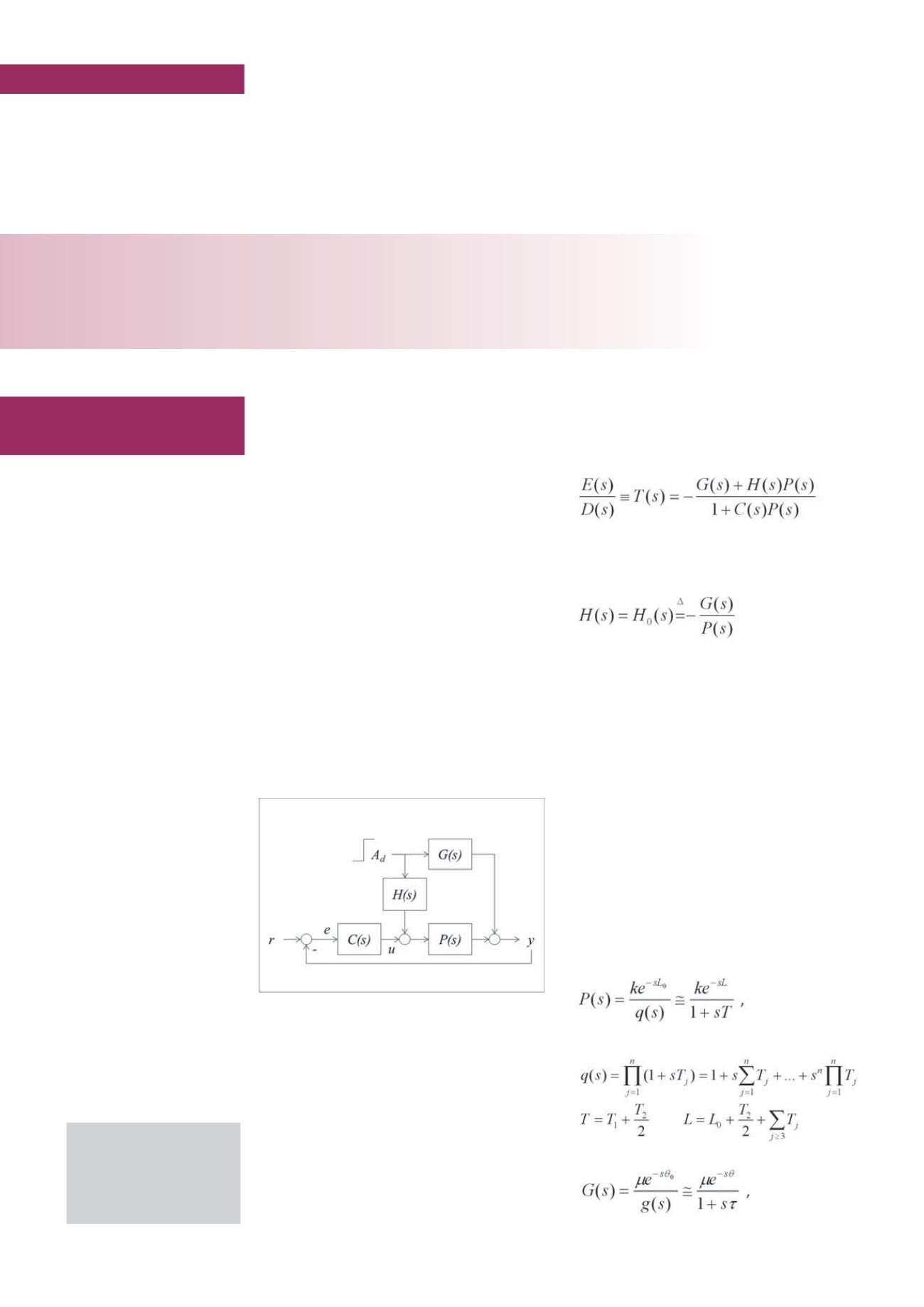
Formalizzando il problema come nella
υ
figura
1
, risulta chiaro che ciò comporta la disponibilità
di una misura addizionale, quella della variabile
di disturbo (
d
), il cui cambiamento, attraverso una
certa dinamica (
G(s)
), influenza la variabile (
y
) di
processo (
P(s)
) che deve viceversa rimanere per
quanto possibile ancorata al suo setpoint (
r
) gra-
zie all’azione (
u
) del regolatore (
C(s)
), al quale
viene appunto in aiuto il compensatore (in anello
aperto)
H(s)
.
Schema classico di compensazione
Da una semplice analisi delle funzioni di trasferi-
mento in gioco, è immediato ricavare che quella
tra il disturbo e l’errore (
e=r-y
) risulta
Per ottenere che l’effetto del disturbo sull’errore
sia nullo, non resta dunque che impiegare
Se il processo è dunque stabile e se il ritardo
contenuto in
G(s)
è maggiore o uguale a quello
contenuto in
P(s)
, allora
H
0
(s)
è realizzabile e
la compensazione ideale può essere implemen-
tata; in realtà anche il grado relativo di
G(s)
deve
essere maggiore o uguale a quello di
P(s)
, altri-
menti il risultato è una funzione di trasferimento
non propria, a meno di trascurare l’eccesso di zeri
a frequenze maggiori.
Spesso funzioni di trasferimento del primo o
secondo ordine con ritardo rappresentano modelli
semplificati ma sufficientemente efficaci per i
processi sotto controllo ed una buona tecnica di
riduzione dell’ordine è costituita dalla “half-rule”
proposta in
[1]
; facendo riferimento alla sua ver-
sione per modelli del primo ordine con ritardo
(FOPDT) si può scrivere:
ove
GLI AUTORI
Massimiliano Veronesi, Yoko-
gawa Italia; Antonio Visioli,
Università di Brescia.
Figura 1 - Schema di compensazione in anello aperto