Un motore matematico per nuove geometrie: Maple e il Gömböc

Maple, il motore di calcolo matematico di Maplesoft, ha contribuito alla scoperta del Gömböc, forma basata sulla matematica. Nel 2007, gli scienziati ungheresi Gábor Domokos e Péter Várkonyi hanno scoperto l’esistenza della forma Gömböc, risolvendo un vecchio mistero. Per anni, infatti, i matematici hanno cercato di dimostrarne l’esistenza attraverso equazioni matematiche. Vladimir Arnold, uno scienziato russo, ne aveva ipotizzato l’esistenza, ma ci sono voluti dieci anni per dimostrarla e creare la forma. Il New York Times ha definito la scoperta “una delle migliori idee dell’anno”.

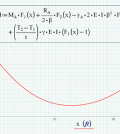
Come in molti altri sviluppi matematici, Maple ha svolto un ruolo importante anche nella creazione del Gömböc. Un Gömböc è un solido tridimensionale omogeneo e convesso che, appoggiato su una superficie piana, ha un punto di equilibrio stabile e uno instabile. La forma Gömböc non è unica; ha infatti innumerevoli varietà, la maggior parte delle quali è molto simile ad una sfera e tutte hanno tolleranze di forma molto rigide (meno di 0,1 mm per 10 cm). La soluzione più famosa presenta la parte superiore a punta, come si vede nella figura.

Se si appoggia un Gömböc su una superficie piana, mettendolo nel suo punto di equilibrio stabile, rimarrà nella stessa posizione. “Anche colpendolo leggermente, ritorna alla sua posizione di riposo nel punto di equilibrio stabile”, afferma Domokos, uno degli inventori del Gömböc. Posizionandolo in un punto di non equilibrio, inizierà a rotolare in modo sistematico finché non raggiungerà il punto di equilibrio stabile. In altri termini, il Gömböc si rimette in piedi da solo (“The story of the Gömböc”, Plus, 2009).  La rivista Wired, infatti, lo ha definito “il primo oggetto al mondo capace di ritornare da solo in posizione eretta”.

Il Gömböc è, inoltre, entrato nel Guinness dei primati come “la prima forma omogena in grado di rimettersi in piedi”. La rivista Natural History spiega che “il segreto è nella matematica della sua forma”.

L’invenzione del Gömböc è stata il culmine di un lungo processo di ricerca matematica e Maple ha svolto un ruolo importante nella sua scoperta. La forma, prima di essere scoperta, era conosciuta come un oggetto mono-monostatico convesso – un oggetto tridimensionale che, a causa della sua geometria, aveva un solo modo possibile per rimanere diritto in equilibrio.

Domokos e Várkonyi hanno identificato una famiglia a due parametri di oggetti, ognuno dei quali dotato della proprietà mono-monostatica desiderata. Tuttavia, non tutti erano convessi. Maple è stato impiegato per identificare le forme convesse e dimostrare quindi l’esistenza della forma. Il processo ha richiesto una grande quantità di calcoli matematici precisi e complessi, resi possibili dalla potenza di calcolo simbolico di Maple.

“La geometria finale del Gömböc doveva essere determinata con grande precisione, i dettagli erano fondamentali e non potevamo permetterci di trascurarne nessuno”, ha affermato Domokos. “Maple è stato molto utile a questo riguardo. L’uso di Maple ha reso i calcoli più precisi e sicuri; la sua potenza computazionale permette di calcolare ed esplorare anche dettagli molto delicati. È stato, quindi, un compagno fidato nel nostro processo di scoperta”.

Parlando della popolarità del Gömböc e dell’attenzione che ha ricevuto dalla comunità scientifica e matematica di tutto il pianeta, Domokos ha inoltre affermato: “La bellezza del Gömböc è la sua assoluta semplicità. È talmente semplice che possono capirlo anche gli studenti delle scuole superiori, ma ha potenzialmente un grande impatto sulla scienza e ha numerose applicazioni in natura. Tuttavia, la soluzione ci è sfuggita per 2000 anni”.

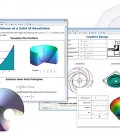
Portando la loro scoperta nel mondo delle scienze naturali, Domokos e Várkonyi hanno individuato un’applicazione eccezionale del Gömböc nel mondo delle tartarughe. I due scienziati hanno condotto uno studio approfondito sulle tartarughe utilizzando complessi modelli tridimensionali del carapace, creati in Maple. Attraverso tali modelli, hanno scoperto che, delle 200 specie di tartarughe in natura, due avevano carapaci a forma di Gömböc. Ciò significava che tali tartarughe avevano un vantaggio evolutivo unico, perché avevano la capacità di rimettersi nella loro posizione naturale.

“Ho visto che si comportavano come Gömböc!” ha esclamato Domokos. Stare sul dorso è una posizione vulnerabile e pericolosa per qualsiasi tartaruga. È noto che il maschio della tartaruga ribalta sul dorso i propri rivali per renderli indifesi. Quindi, qualsiasi tartaruga che sia capace di ritornare sulla sua pancia, grazie alla gravità e senza dovere utilizzare i suoi muscoli, ha un vantaggio unico e una maggiore potenza. “È la forma Gömböc del carapace che offre loro tale potenza. Questo è un classico esempio di evoluzione attraverso la ricerca della forma ottimale per la sopravvivenza”, ha osservato Domokos.

A continuazione della sua ricerca, Domokos è attualmente impegnato nello studio della forma dei ciottoli che si trovano sulle spiagge. La sua ricerca, condotta insieme a Gary Gibbons dell’Università di Cambridge, cerca di descrivere la forma dei ciottoli e la sua evoluzione. I due stanno anche cercando di comprendere l’interazione fra i ciottoli nella loro evoluzione collettiva.

Grazie a Maple, Domokos è riuscito a studiare un sistema di equazioni differenziali integrabili. Risolvere sistemi di equazioni gli offre una prospettiva unica su dettagli che altrimenti si perderebbero. Lo scienziato sta anche studiando l’equilibrio dell’attrito e delle collisioni nel processo di abrasione che provoca i cosiddetti rapporti dominanti fra i ciottoli, un fenomeno grazie al quale i ciottoli in una certa area geografica presentano caratteristiche geometriche globali simili. Domokos sta utilizzando Maple per determinare i coefficienti di attrito critici che sono responsabili del manifestarsi di rapporti dominanti fra i ciottoli.

Capire le forme in natura sta diventando sempre più importante, sia sulla Terra che nello spazio. Recentemente, il rover Curiosity della NASA ha trasmesso immagini della superficie di Marte che mostravano il letto di un vecchio fiume. Le dimensioni e la forma dei ciottoli indicano che su Marte, miliardi di anni fa, c’era l’acqua. Inoltre, studiando le immagini delle rocce, gli scienziati saranno in grado di saperne di più sulla velocità e sulle dimensioni dell’antico corso d’acqua.

Dato che Domokos sta proseguendo la sua ricerca sulle forme matematiche e la scoperta di fenomeni naturali e scientifici basati su tali forme, anche Maple continuerà a svolgere un ruolo significativo in tale ricerca. “Maple è il mio strumento di calcolo preferito, è semplice e potente”, afferma Domokos. “Siamo circondati da forme geometriche che i nostri cervelli non sono pronti a capire. Forme come il Gömböc danno vita ad un nuovo linguaggio per comprendere tali forme”.

Contenuti correlati

• 
  MapleSim Connector semplifica lo sviluppo di macchine sfruttando la modellazione

  B&R MapleSim Connector è disponibile all’interno dell’ambiente B&R Automation Studio e rende quindi estremamente semplice l’integrazione dello strumento MapleSim di Maplesoft. MapleSim crea un modello altamente accurato e dinamico della macchina basato su dati CAD in formato...
• 
  Sviluppo più efficiente con i digital twin

  B&R MapleSim Connector è disponibile all’interno dell’ambiente B&R Automation Studio e rende quindi estremamente semplice l’integrazione dello strumento MapleSim di Maplesoft. MapleSim crea un modello altamente accurato e dinamico della macchina basato su dati CAD in formato...
• 
  Ptc aggiorna il software di calcolo Mathcad Prime

  Ptc presenta l’ultima versione del proprio software di calcolo Mathcad Prime. Le nuove funzioni di Ptc Mathcad Prime 4.0 permettono all’utente di mostrare, risolvere e proteggere i dati in modo più efficace, incrementandone anche il valore e...
• 
  solidThinking: ecco la nuova suite software per applicazioni di ingegneria

  solidThinking ha rilasciato una nuova suite software per le applicazioni di ingegneria e per la progettazione multidisciplinare/multifisica. La nuova suite basata su un’approccio “model-based”, promuove l’innovazione attraverso la simulazione combinando la modellazione matematica, fisica, di segnale e...
• 
  Arrivano gli ambasciatori di Maple

  Maplesoft ha annunciato il programma Maple Ambassador, progettato per offrire una maggiore influenza e visibilità sullo sviluppo del software agli appassionati di Maple, che potranno candidarsi sul sito per diventare ambasciatori. Un Maple Ambassador ufficiale ispirerà ed educherà...
• 
  Nuova release Maple 2015

  Con Maple 2015, la nuova release del software di calcolo matematico per l’insegnamento, la ricerca e lo sviluppo a contenuto matematico, l’ingegneria e le scienze, Maplesoft offre nuove importanti possibilità sia ai docenti che ai ricercatori nelle...
• 
  Più integrazione e nuove funzionalità per PTC Mathcad Prime 3.1

  PTC ha reso disponibile il software di progettazione e calcolo ingegneristico PTC Mathcad Prime 3.1, studiato per i tecnici che devono analizzare, risolvere, documentare e condividere calcoli e concetti di fondamentale importanza. Grazie a questa nuova versione,...
• 
  L’Università di Waterloo e Maplesoft insieme per la formazione online: ecco la piattaforma

  L’Università di Waterloo (UW) e Maplesoft hanno annunciato una partnership che ha come obiettivo la formazione online e la nascita di corsi di scienze, tecnologia, ingegneria e matematica (STEM). Da questa collaborazione è nata la piattaforma per...
• 
  Nuovi tool in MapleSim per lo studio dei progetti

  La nuova versione di MapleSim, l’avanzata piattaforma di modellazione e simulazione a livello di sistema di Maplesoft, facilita l’esplorazione e la validazione dei progetti, la creazione e gestione di librerie di componenti custom e l’uso dei modelli...
• 
  MapleSim, l’ultima release aumenta le capacità del control design

  Maplesoft annuncia un importante aggiornamento del MapleSim Control Design Toolbox, un add-on di MapleSim, l’avanzato tool di modellazione e simulazione a livello di sistema di Maplesoft. Il MapleSim Control Design Toolbox permette di sfruttare la maggiore flessibilità...