
Ottobre 2015
n
Automazione e Strumentazione
CONTROLLO
tecnica
80
risulta efficacemente robusto nei confronti del rumore di misura.
Calcolati così matematicamente i parametri del processo, stimati
i ritardi puri
q
jj
come i tempi necessari agli errori per uscire dalla
soglia di rumore e infine ricavati per differenza le costanti di
tempo
si può procedere a taratura automatica dei regolatori ricavando
le formule seguenti dall’approccio proposto in
Lee et alii
[1]
per
algoritmo PID in versione parallelo:
Queste formule di taratura (non esplicitate in
Lee et alii
[1]
) si
ricavano imponendo che le funzioni di trasferimento in anello
chiuso tra ogni riferimento
R
j
e il relativo processo
P
j
siano di tipo
FOPDT con costante di tempo pari a
l
1,2
e si basano sulla espan-
sione in serie di McLaurin del modello del processo. Si noti che
nel tempo integrale interviene un fattore di correzione (il valore
a regime del
j-esimo
elemento diagonale della matrice inversa di
quella del processo, in modo da tener conto (attraverso il deter-
minante) anche delle interazioni tra gli anelli di regolazione; ciò
è ragionevole se si considera che sia l’effetto del tempo integrale
che quello delle interazioni dovrebbero essere rilevanti alle basse
frequenze. Qualora si voglia favorire la robustezza a scapito della
reattività del controllore, scegliere come costante di tempo in
anello chiuso (
l
1,2
) un valore maggiore del ritardo apparente (
q
jj
).
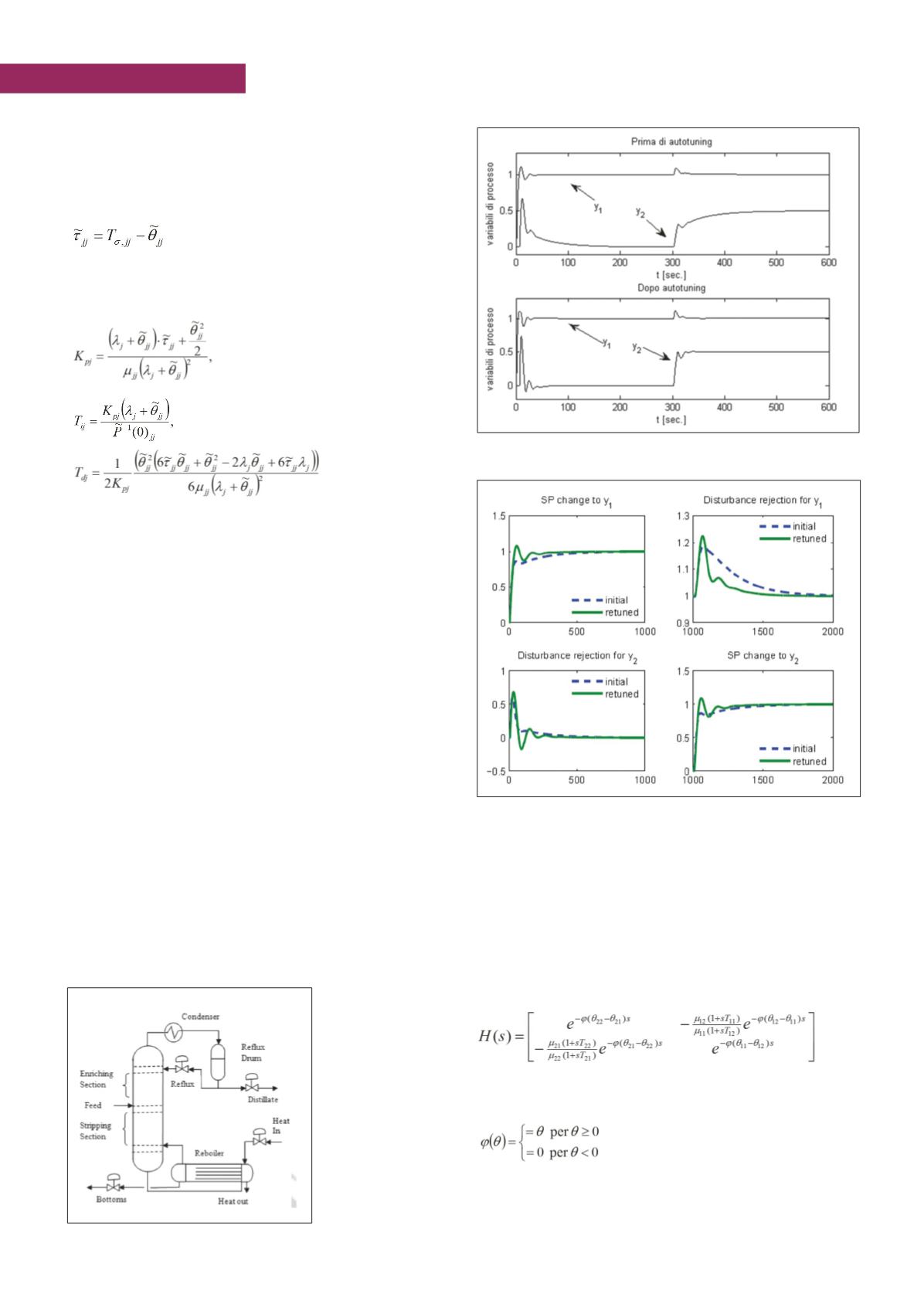
Un esempio delle prestazioni ottenibili è illustrato nella
►
figura
5
, relativamente a un modello FOPDT di colonna di distillazione
binaria (metanolo/acqua) largamente usato come caso di processi
interagenti (si veda
Luyben
[3]
); le variabili controllate sono le
composizioni di testa (distillato) e di fondo mentre quelle di con-
trollo sono le portate di reflusso e di vapore nel ribollitore (cfr
►
figura 4
).
Un altro esempio è illustrato in figura 6, relativamente al modello
FOPDT di colonna riportato in
A.S. Rao et alii
[4]
; in tal caso per
il retuning è stato scelto
l
j
=4
q
jj
.
La tecnica proposta può essere opportunamente estesa anche in
presenza di un disaccoppiatore ovvero un blocco
H(s)
posto tra i
controllori e il processo e progettato in modo che il prodotto
P(s)
H(s)
sia una matrice diagonale. Uno dei più diffusi e applicati
disaccoppiatori è quello proposto in
Wang et alii
[5]
: ipotizzando
che ogni processo coinvolto sia ben rappresentato da un modello
di tipo FOPDT (ricavabile per esempio come proposto in questo
contributo) il disaccoppiatore risultante è espresso come
ove la funzione
j
(•)
è definita come
In tal caso però, facendo riferimento alla
►
figura 7
, i guadagni
che si ricavano sulla base degli integrali dell’errore sono quelli
della matrice
P(s)H(s)
, pertanto quelli del processo vero e proprio
Figura 6 - Effetto dell’autotuning sul modello di colonna Wardle & Wood
Figura 4 - Schema di
colonna di distillazione
con ribollitore
~
~
Figura 5 - Effetto dell’autotuning sul modello di colonna Wood & Berry


















