
controllo
tecnica
Ottobre 2015
n
Automazione e Strumentazione
76
mente semplificata, è che la somma degli elementi
di una generica riga o colonna è sempre pari a uno
e in ogni caso essa può essere ottenuta a partire
dalla matrice dei
M
guadagni come
G=M
⊗
(M
-1
)
T
.
Nel caso di un sistema 2x2 comunque si otten-
gono semplicemente:
È evidente che se si ha
g
11
=g
22
=1
(e quindi
g
12
=g
21
=0
), allora non
vi è alcuna interazione tra i due
loop
di controllo e l’accoppia-
mento è inesistente, per cui si possono considerare separatamente
due schemi a singolo ingresso e a singola uscita. Se invece gli ele-
menti della diagonale principale della matrice dei guadagni relativi
non sono significativamente maggiori degli altri allora sarà molto
arduo tentare di controllare il processo attraverso degli anelli di
regolazione indipendenti (controllo decentralizzato).
La
►
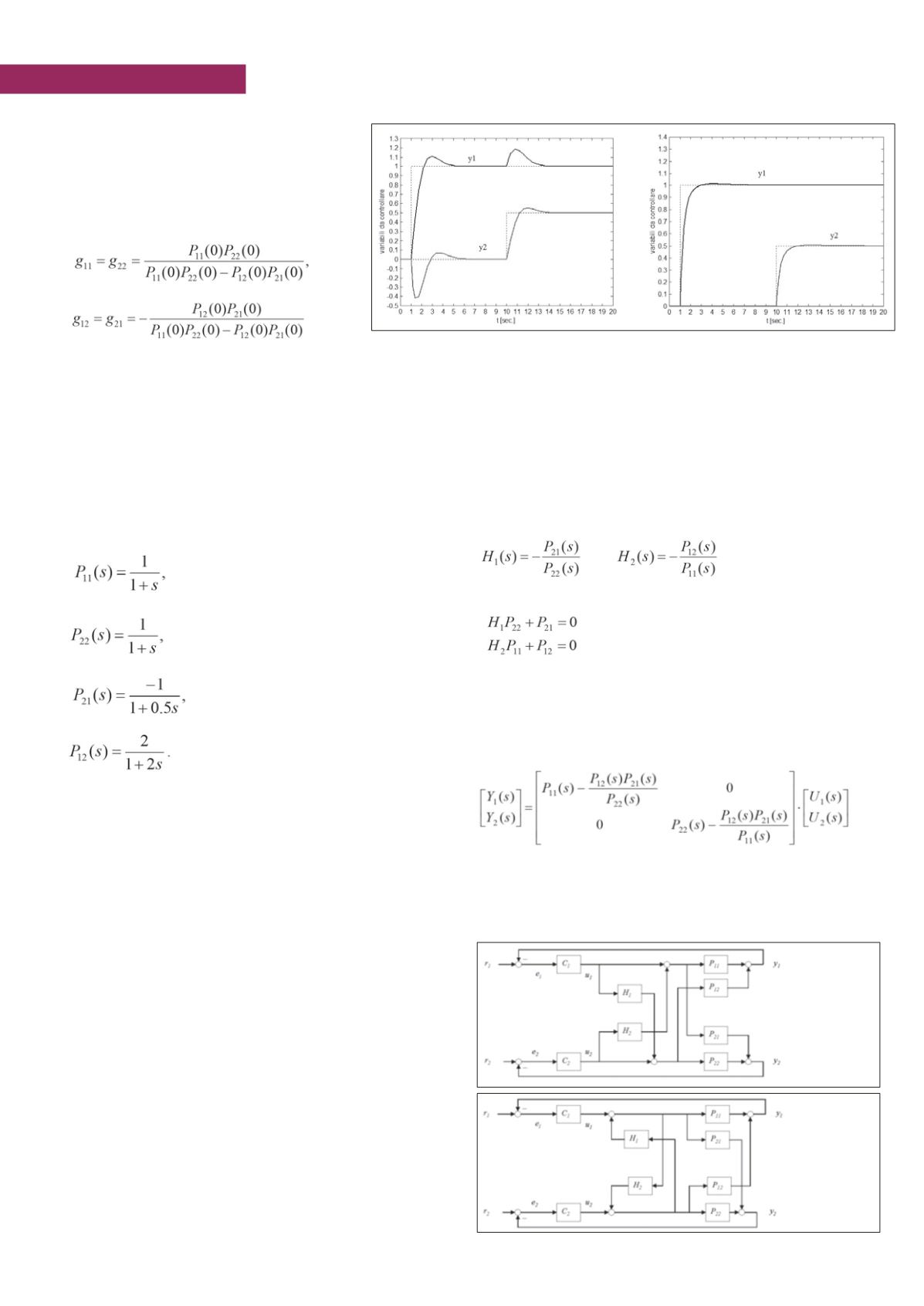
figura 2
si riferisce al semplice caso ipotetico in cui
con i due
setpoint
che subiscono una variazione rispettivamente
unitaria e semi-unitaria. Si nota in particolare che, a causa dell’in-
terazione, le variabili da controllare deviano dal rispettivo
setpoint
anche quando questo rimane costante. La matrice dei guadagni
relativi è molto utile quindi nella scelta degli accoppiamenti tra le
variabili di ingresso e quelle di uscita nel sistema di controllo. Si
dovrà infatti cercare di accoppiare gli ingressi e le uscite in modo
che i guadagni relativi corrispondenti siano positivi e il più pos-
sibile prossimi a uno. In generale, se si ha
0<g
11
=g
22
<1
, allora
il guadagno in anello chiuso tra
u
1
e
y
1
è maggiore di quello in
anello aperto, per cui è necessario diminuire i guadagni del regola-
tore (detuning) per mantenere la stabilità del sistema complessivo
(e i guadagni relativi possono essere impiegati come fattore di
detuning). Se invece si ha
g
11
=g
22
>1
, allora vale il ragionamento
opposto e teoricamente sarebbe possibile addirittura aumentare i
guadagni del regolatore grazie all’accoppiamento, scelta allettante
(specialmente per la reiezione dei disturbi additivi) ma tuttavia
sconsigliata in casi pratici, dal momento che un’eventuale aper-
tura del secondo anello di controllo potrebbe a questo punto por-
tare il primo all’instabilità. Infine, fortemente da evitare è il caso
in cui
g
11
=g
22
<0
, dal momento che la chiusura del secondo anello
porterebbe il primo a un cambiamento di segno nella retroazione
con conseguente perdita di stabilità.
Si tenga presente che in generale la stabilità complessiva del
sistema risulta determinata dagli zeri della funzione di trasferi-
mento
(1+C
1
P
11
)(1+C
2
P
22
)-C
1
C
2
P
12
P
21
.
Per migliorare le prestazioni può essere quindi opportuno utiliz-
zare uno schema di disaccoppiamento come quello illustrato nella
►
figura 3
, relativamente al sistema 2x2. Si tratta semplicemente
di utilizzare delle opportune azioni in avanti (feedforward) attra-
verso le funzioni di trasferimento
in modo tale che risulti
e quindi che sia non nulla l’influenza delle uscite dei regolatori
PID solo su una delle variabili controllate.
A questo punto i due
loop
possono considerarsi non più intera-
genti e i due algoritmi PID possono essere tarati considerando che
la matrice delle funzioni di trasferimento è diventata
La precedente
►
figura 2
illustra anche i risultati ottenibili con lo
schema della
►
figura 3
, radicalmente migliori, sempre in rife-
rimento allo stesso sistema complessivo e ovviamente a parità di
parametri PID.
Figura 2 - Anelli interagenti senza (sinistra) e con (destra) disaccoppiamento
Figura 3 -
Schemi per il
disaccoppiamento
in avanti e
all’indietro
►


















