AS_2-2018

CONTROLLO

tecnica

Automazione e Strumentazione

Marzo 2018

tion to the disturbance means high overshoot in the response

to setpoint step change. This is very common when zero-pole

cancellation tuning is applied: the cancellation works fine for

the tracking task but the poles of the process are still there in the

transfer function between the load disturbance and the process

variable. The typical situations are summarized in the table.

Trade-off between performance and robustness

Another important trade-off is the one between performance and

robustness. The robustness is a measure of how much the con-

troller can tolerate changes in the process transfer function; more

specifically, in its gain and in its phase lag.

Also in this case there are some useful parameters which can be

used as design criteria for robustness:

- The gain margin is a measure of how much the process gain

can change (typically, increase) before the closed loop system

become unstable; the control theory says it is the amount of

gain increase or decrease required to make the loop gain unity

at the frequency where the phase angle is -180°; more accu-

rately, it is the maximum factor by which the process gain can

be multiplied before the closed loop become unstable.

- The phase margin (

) is a measure of how much the pro-

cess phase can change (typically, increase) before the closed

loop system become unstable; the process critical phase

could be increased because of an additional delay (dead-

time, due, for example to friction in the valve) or because

the process lag decrease (due, for instance, to a change in

the fluid properties or in the reaction speed); from the con-

trol theory the maximum delay that could be tolerated by the

loop is =

(where is the critical pulse corresponding to

the point where the Nyquist diagram enter in the unit circle).

Furthermore, it’s interesting to remark that when the closed

loop system starts being represented by a second order

oscillating system, its damping is somehow proportional to

the phase margin.

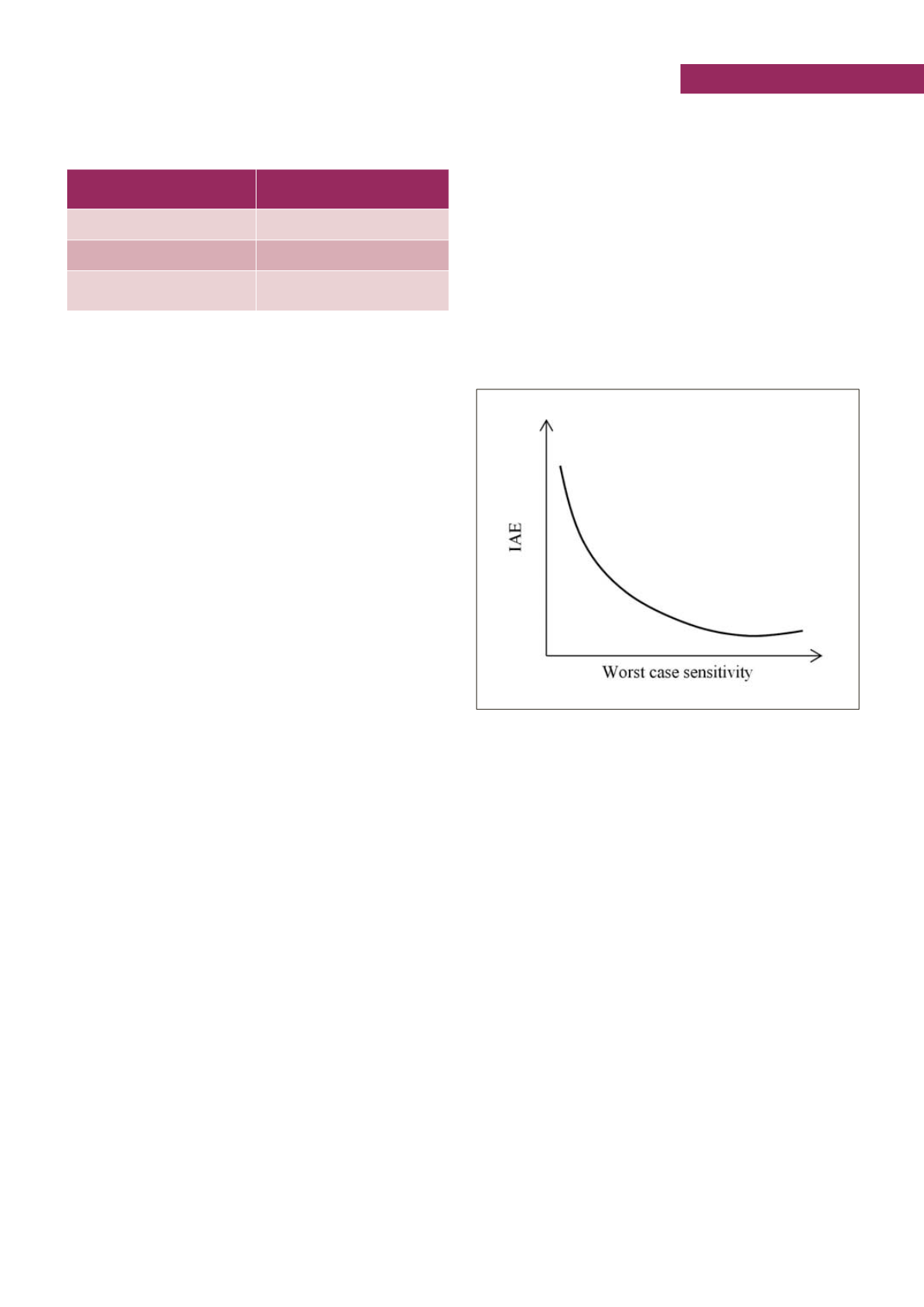
One interesting single parameter for evaluating the robustness is

the so called worst case sensitivity, given by the shorter distance

from the Nyquist diagram to the real point -1; this maximum sen-

sitivity is strictly related to the gain and phase margin through

some simple inequalities.

Through this single parameter it’s not difficult represent-

ing the trade-off between performance and robustness as it

happens in the figure (which is referred to a simple specific

FOPDT process); of course the trade-off does not continue so

much on the right because as soon the Nyquist diagram start

approaching to (-1, 0i) the behavior becomes oscillating and

IAE increases again.

Additional considerations should be made about the measure-

ment noise filtering and the control action effort. The closed loop

system acts more or less ad a low-pass filter with unit gain and

bandwidth equal to [0

]; therefore

should be set high enough

to allow fast setpoint changes and quick reaction to disturbances

but not so much to let the measurement noise affect the control

action: for not stressing or saturate the actuator, the controller

C(j ) should not have high values for >

. So it clear that we

have a trade-off again.

Solutions and Conclusions

In order to resolve the trade-off, some countermeasures can be

adopted. One solution is implementing a

two degree of free-

dom

(2DoF) controller where the ordinary PID parameters can

be tuned for good disturbance rejection but an additional set-

point weight allows to attenuate the overshoot in the setpoint

following task. Where the 2DoF algorithm is not available, set-

point changes should be ramp instead of step.

Another solution is employing

different sets of PID parameters

depending by the task or the situation to cope with. The default

set should be for providing an effective reaction to the unpre-

dictable disturbances; then a different set can be recalled any

time setpoint change is given by the operator or by a sequence

currently under execution. When it is known the plant unit is

going to work in unusual conditions different from the nominal

process design, then a set of robustness-oriented PID parame-

ters can be copied in the controller memory.

The PID algorithm is one of the simplest solutions to control

problems but it cannot provide effective results for different

kind of performance and goals; it is worth focusing on

the more

relevant task

and selecting the set of parameters more appro-

priate for it; alternatively some a bit more complex techniques

can be implemented in order to make the PID controller effec-

tive in different operating conditions.

Example Typical Trade-off between robustness and performance

Setpoint following

(tracking problem)

Load disturbance rejection

(regulation problem)

Slow with no overshoot

Sluggish

Fast with poor overshoot

Quiet reaction with no overshoot

Fast with large overshoot

and oscillations

Fast reaction with poor overshoot

Typical situations occurring during PID tuning procedures